4. Determination of heat of solution (DHS) by calorimetric method.
5. Determination of heat of reaction (DHR) by calorimetric method.
6. Measurement of water equivalent of a calorimeter.
7. Determination of specific heat of a liquid by calorimetric method.
Click here
https://docbrown.info/page07/delta1Hc.htm
-------------------------------------------------------------------------------------------
Heat of Solution or Enthalpy of Solution Chemistry Tutorial
Key Concepts
⚛ A solute dissolves in excess solvent to form a solution:
solute + solvent → solution
⚛ Heat of solution, or, enthalpy of solution, is the energy released or absorbed when the solute dissolves in the solvent.
⚛ Molar heat of solution, or, molar enthalpy of solution, is the energy released or absorbed per mole of solute being dissolved in solvent.
⚛ Heat of solution (enthalpy of solution) has the symbol(1) ΔHsoln
⚛ Molar heat of solution (molar enthalpy of solution) has the units(2) J mol-1 or kJ mol-1
⚛ If heat is released when the solute dissolves, temperature of solution increases, reaction is exothermic, and ΔH is negative (ΔH < 0).
solute + solvent → solution ΔHsoln = −
solute + solvent → solution ΔHsoln < 0
⚛ If heat is absorbed when the solute dissolves, temperature of solution decreases, reaction is endothermic, and ΔH is positive (ΔH > 0).
solute + solvent → solution ΔHsoln = +
solute + solvent → solution ΔHsoln > 0
⚛ Enthalpy (heat) of solution can be determined in the laboratory by measuring the temperature change of the solvent when solute is added.
⚛ To calculate the molar enthalpy of solution (molar heat of solution) using experimental data:
Step 1: Calculate the amount of energy released or absorbed (q)
q = m × Cg × ΔT
q = amount of energy released or absorbed
m = mass
Cg = specific heat capacity
ΔT = change in temperature
Step 2: Calculate moles of solute (n)
n = m ÷ M
n = moles of solute
m = mass of solute
M = molar mass of solute
Step 3: Calculate mount of energy (heat) released or absorbed per mole of solute (ΔHsoln)
ΔHsoln = q ÷ n
ΔHsoln = molar enthalpy (heat) of solution
q = amount of energy (heat) released or absorbed
n = moles of solute
Note: You must include the sign for ΔHsoln (either + or −)
(i) ΔH is negative if energy (heat) is released (exothermic).
(ii) ΔH is positive if energy (heat) is absorbed (endothermic).
Please do not block ads on this website.
No ads = no money for us = no free stuff for you!
Theory Behind Determining Molar Enthalpy of Solution
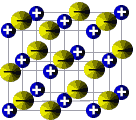
The molecules or ions making up a solid solute exist in a highly ordered state which is referred to as a lattice.
You are probably already familiar with representations of ionic compounds in which positive ions (cations) and negative ions (anions) are arranged in a lattice held together by electrostatic forces of attraction known as ionic bonds.
The amount of disorder, or randomness, in a system is known as its entropy. A lattice is highly ordered, that is, the particles making up the lattice are in a low state of disorder. This is referred to as a low entropy state(3).
When this solute dissolves in a solvent, particles such as ions must be removed from the lattice and each solute particle must then be completely surrounded by solvent molecules.
The solute particles in the solution are in constant motion and distributed more or less randomly throughout the solution so that the amount of disorder has increased compared to when they were part of the lattice. Solute particles in the solution are said to be in a higher state of entropy than solute particles making up the lattice.
The process of dissolving a solid solute in a liquid solvent can therefore be thought of as occurring in two steps:
| Step 1: A particle of solute, such as an ion or molecule, breaks away from the lattice. | Step 2: The solute particle is surrounded by solvent molecules. | |
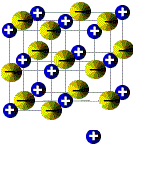 | 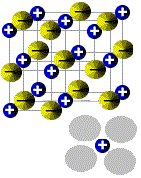 | |
| Lattice energy, ΔHlat, is the energy required to break up the crystal lattice. Breaking up the lattice is an endothermic process. | Solvation energy, ΔHsolv is the energy released or absorbed when solute particles are completely surrounded by solvent molecules. When water is used as the solvent, we use the term hydration energy, ΔHhyd, rather than the more general term solvation energy. Hydration is usually exothermic, so heat is released when water molecules completely surround solute particles. | |
| ΔHlat > 0 | ΔHhyd < 0 |
If Enthalpy of Solution (heat of solution) is Endothermic:
The magnitude of the energy absorbed to break up the lattice, ΔHlat, is greater than the magnitude of the energy released when solute particles are surrounded by water solvent molecules, ΔHhyd, so the enthalpy of solution, ΔHsoln, is positive, that is, the process is endothermic.
if |ΔHlat| > |ΔHhyd| then ΔHsoln is positive
solute(s) + water(l) → solution(aq) ΔHsoln = + solute(s) + water(l) + ΔHsoln → solution(aq) Energy is absorbed, that is, energy is a reactant. When solute is added to water, water temperature decreases. |
|
If Enthalpy of Solution (heat of solution) is Exothermic:
The magnitude of the energy absorbed to break up the lattice is less than magnitude of the energy released when solute particles are surrounded by water solvent molecules , so the enthalpy of solution is negative, that is, the process is exothermic.
if |ΔHlat| < |ΔHhyd| then ΔHsoln is negative
solute(s) + water(l) → solution(aq) ΔHsoln = - solute(s) + water(l) → solution(aq) + ΔHsoln Energy is released, that is, energy is a product. When solute is added to water, water temperature increases. |
|
The table below lists the values of molar enthalpy of solution (molar heat of solution) for some common salts in water at 25°C.(4)
| Molar Enthalpy of Solution of Some Salts at 25°C | |||||
|---|---|---|---|---|---|
| Endothermic examples | Exothermic examples | ||||
| Anion | solute | ΔHosoln (kJ mol-1) | solute | ΔHosoln (kJ mol-1) | |
| chloride | NH4Cl(s) | +14.78 | LiCl(s) | -37.03 | |
| NaCl(s) | +3.88 | ||||
| KCl(s) | +17.22 | ||||
| bromide | NH4Br(s) | +16.78 | LiBr(s) | -23.26 | |
| KBr(s) | +19.87 | NaBr(s) | -0.60 | ||
| nitrate | NH4NO3(s) | +25.69 | LiNO3(s) | -2.51 | |
| AgNO3(s) | +22.59 | ||||
| NaNO3(s) | +20.50 | ||||
| KNO3(s) | +34.89 | ||||
| hydroxide | LiOH(s) | -23.56 | |||
| NaOH(s) | -44.51 | ||||
| KOH(s) | -57.61 | ||||
| acetate | NH4C2H3O2(s) | -2.38 | |||
| NaC2H3O2(s) | -17.32 | ||||
| KC2H3O2(s) | -15.33 | ||||
Experiment to Determine the Molar Heat of Solution (Molar Enthalpy of Solution) of a Solute
The following describes the use of a polystyrene foam (styrofoam™) cup as a calorimeter to determine the heat of solution of a salt (solid solute) in water (the solvent).(5)
Polystyrene foam (styrofoam™) is a good insulator, that is, it is a material that does not conduct heat well.
In this experiment the polystyrene foam (styrofoam™) cup is used as an insulated vessel in which to conduct the experiment so that either:
(i) all the energy released by the reaction is used to raise the temperature of the water in the cup and is not lost in heating the surrounding environment in the case of an exothermic reaction
(ii) the only energy being absorbed by the reaction is that from the water in the cup and not from the surrounding environment in the case of an endothermic reaction.
Procedure:
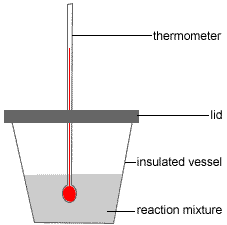
- Step 1: An accurately known quantity of water (the solvent) is placed in a well insulated vessel (eg, a polystyrene foam or styrofoam™ cup)
- Step 2: The initial temperature of this solvent is recorded, Ti.
- Step 3: An accurately known quantity of the solid solute is added, the vessel is sealed with a lid and the solution stirred using the thermometer.
- Step 4: The final temperature of the solution is recorded, Tf.
Note the final temperature will be the maximum temperature reached for an exothermic reaction or the minimum temperature reached for an endothermic reaction.
Calculation of Molar Enthalpy of Solution (molar heat of solution) (6)
Step 1: Calculate the heat released or absorbed, in joules, when the solute dissolves in the solvent:
heat released or absorbed = mass × specific heat capacity × change in temperature
q = m × cg × (Tfinal - Tinitial)
q = m × cg × ΔT
| What is the value of mass, m? There are 2 ways to look at this: | ||
| 1. Method usually used by High School courses. Assume all the solute dissolves simultaneously in the solvent so that all the heat is simultaneously absorbed from, or released to, the pure solvent. m = mass of solvent in grams So, cg = specific heat capacity of the solvent in J°C-1g-1 ΔT = Tfinal - Tinitial in °C(7) When calculated, q is in joules (J) | OR | 2. Method usually used in introductory University courses. Assume the first molecule or ion of solute dissolves into pure solvent, but each subsequent molecule or ion is dissolving into a mixture of dissolved solute in solvent (that is, a solution). In this case, the final solute molecule or ion is dissolving into a solution with a mass approximated by the mass of the solvent plus the mass of the solute. m = mass of solvent + mass of solute in grams So, cg = specific heat capacity of the solution in J°C-1g-1 ΔT = Tfinal - Tinitial in °C(7) When calculated, q is in joules (J) |
Step 2: Calculate moles of solute:
where:
moles = amount of solute in mole
mass = mass of solute in grams
molar mass = molar mass of solute in grams per mole
Step 3: Calculate the molar enthalpy of solution, or molar heat of solution, ΔHsoln:
| ΔHsoln in J per mole of a solute is calculated: | ΔHsoln in kJ per mole of a solute is calculated: |
|---|---|
| ΔHsoln = q ÷ moles of solute (J mol-1) where exothermic reactions: ΔHsoln is negative endothermic reactions: ΔHsoln is positive | ΔHsoln = q/1000 ÷ moles of solute (kJ mol-1) where exothermic reactions: ΔHsoln is negative endothermic reactions: ΔHsoln is positive |
Worked Example: Sample Experimental Results and Calculations
A student added 4.00 g of NaOH(s) to 100 g of water in a polystyrene foam cup.
The temperature of the water rose by 10.0°C.
Assuming the polystyrene foam cup is well insulated and the specific heat capacity of water is 4.18 J°C-1g-1, determine the molar enthalpy of solution of sodium hydroxide in kJ mol-1.
Solving the Problem using the StoPGoPS model for problem solving:
| STOP | STOP! State the Question. | |||||||||||||||||||||||||||||||||
| What is the question asking you to do? Calculate the molar heat of solution of sodium hydroxide in kJ mol-1 ΔHsoln = ? kJ mol-1 | ||||||||||||||||||||||||||||||||||
| PAUSE | PAUSE to Prepare a Game Plan | |||||||||||||||||||||||||||||||||
| (1) What information (data) have you been given in the question? m(NaOH) = mass NaOH(s) = 4.00 g m(H2O) = mass H2O(l) = 100 g ΔT = temperature increase = 10.0°C cg(H2O) = specific heat capacity of water = 4.18 J°C-1g-1 (2) What is the relationship between what you know and what you need to find out?
Note: ΔHsoln will be negative because the temperature increased, that is, the process is exothermic. | ||||||||||||||||||||||||||||||||||
| GO | GO with the Game Plan | |||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||
| PAUSE | PAUSE to Ponder Plausibility | |||||||||||||||||||||||||||||||||
| Is your answer plausible? Work backwards:
Since this value for the change in temperature is the same as that given in the question, we are confident our answer is correct. | ||||||||||||||||||||||||||||||||||
| STOP | STOP! State the Solution | |||||||||||||||||||||||||||||||||
| State your solution to the problem. Method 1: Molar enthalpy of solution of sodium hydroxide is −41.8 kJ mol-1 Method 2: Molar enthalpy of solution of sodium hydroxide is −43.5 kJ mol-1 | ||||||||||||||||||||||||||||||||||
Register your group.
Sample Question
A student added 1.92 g of KBr(s) to 100 g of water in an insulated vessel. The temperature of the water fell by 0.766°C. Calculate ΔHsoln in kJ mol-1.
Footnotes:
(1) If the solute and the solvent are in their standard states, you can also write ΔHosol
Refer to Standard Enthalpy (heat) of Formation and Reaction
(2) You may also units of cal mol-1 or kcal mol-1
1 calorie = 4.18 joules
1 cal = 4.18 J
For conversions between J, kJ, and cal refer to energy conversions
(3) Entropy refers to the amount of disorder, or randomness, in a system.
Ions locked into a crystal structure are in a low state of disorder and therefore have low entropy.
Ions moving randomly through the solvent molecules in a solution are much more disordered, much more random, so they are said to be in a higher state of entropy.
Gas molecules moving randomly in the atmosphere are in an even greater state of disorder or randomness, so they are said to have an even higher state of entropy.
Moving towards a higher state of entropy is one of the driving forces for a chemical reaction.
(4) The values given are for solutions at infinite dilution which is the enthalpy change when 1 mole of solute in its standard state is dissolved in an infinite amount of water.
(5) Go to Calorimetry Tutorial to see an alternative method used an adiabatic solution calorimeter.
(6) On this page the calculations assume that there is a large excess of solvent
Note that the following examples all use the specific heat capacity of the solvent, cg, not molar heat capacities, C.
(7) You can use other units for temperature.
If you use Kelvin (K), then cg will have the same numbers but the units change to JK-1g-1. This because a change of temperature of 1K is the same as the change of temperature of 1°C.
If you use fahrenheit then you will have to use a value for cg that has the units J°F-1g-1
---------------------------------------------------------
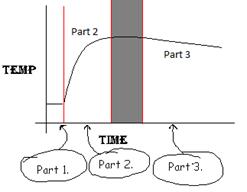
Explanation of the Graph: Below is a general temperature vs. time graph representative for all reactions trials done for this experiment. (Figure A-2) It is divided into three parts.
NOTE: the dark band between Part 2 and Part 3 is a transition area that is not usable for data analysis. The linear regression is done on part 3 to the right of this dark area!
Figure A-2. A general temperature vs. time graph
Part 1. This is the initial temperature. Only one reactant is in the solution and so our reaction is not happening. (For example, for Mg, only 25.0 ml of HCl and 35.0 ml of water are in the solution.) Between part 1 and part 2 the reactants are mixed together.
Part 2. The temperature is changing rapidly. Both reactants are now in the solution and are reacting to give off heat. (For example, for Mg, this is because the Mg turnings are added to the solution.) Somewhere within the blocked out region the reaction stops.
Part 3. The reaction has already stopped. Since the calorimeter isn’t a perfect insulator, heat is lost to the environment and, as a result, the temperature decreases. The temperature should be constantly decreasing. (For example, for Mg, all of the Mg has been converted to Mg2+.)
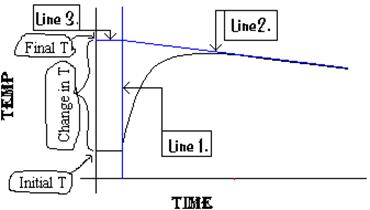
How do you get DT? DT is equal to the extrapolated final temperature minus the solutions initial temperature. So DT = Tf – Ti. Below is the same general graph from figure 1, but it has been extrapolated to find Tf (Figure 2). Tf can also be determined by doing a linear regression on the linear, right hand side of the curve to determine the slope and y-intercept of line 2 and then solving for the temperature using the time at the start of the reaction (line 1).
Figure A-3. Extrapolation of a Temperature vs. Time Graph to Find DT.
Line 1. This line represents the time when the reactants were mixed and so the start of the reaction.
Line 2. This line helps us model what the final temperature would be if the reaction and temperature measurement were instantaneous. It compensates for the heat lost from the calorimeter so that we can estimate the final temperature if the reaction and temperature measurement were instantaneous. This line is important because it compensates for heat lost to the environment while temperature is measured during and after the reaction.
Line 3. This line is drawn at a right angle to line 1 to intersect the point where lines 1 and 2 meet. It is there to help read the final temperature, Tf, at the y-axis.
---------------------------------------------------------
1.3 Experimental methods for determining enthalpy changes and treatment of results
Page introduction
This page describes experimental methods for determining enthalpy changes of chemical reactions e.g. using a simple calorimeter and a bomb calorimeter.
Treatment of experimental results is covered i.e. how to calculate the molar enthalpy for the reaction under investigation.
See also a set of enthalpy problems to solve, worked out answers given on a separate page!
1.3a Experimental methods
All the methods described here rely on measuring a temperature change knowing the molar quantities of reactants and the mass of water used in a calorimeter system
1.3a1 A simple polystyrene calorimeter of low heat capacity can be used for any non–combustion reaction that will happen spontaneously at room temperature involving solutions or solid reacting/dissolving with/in a liquid like water and it doesn't matter if the reaction is exothermic or endothermic.
Reasonably accurate results can be obtained for a school/college laboratory. The reactants are weighed in if solid and a known volume of any liquid (usually water or aqueous solution). The mixture could be a salt and water (heat change on dissolving) or an acid and an alkali solution (heat change of neutralisation). It doesn't matter whether the change is exothermic (heat released or given out, temperature increases) or endothermic (heat absorbed or taken in, temperature decreases).
Ideally a very accurate mercury thermometer with 0.1 or 0.2 oC graduations should be used or an equally accurate electronic digital thermometer (can read to 0.01oC via a thermistor, a solid–state electronic device).
A double polystyrene cup system provides good thermal insulation for the system.
Typical apparatus needed for this kind of calorimetric work with a simple polystyrene cup calorimeter
Safety spectacles, pipette and suction pipette filler (or a burette, double polystyrene cup calorimeter with insulating lid plus hole for the thermometer or temperature probe, chemicals of appropriate mass/volume/concentration, weighing bottle, spatula, accurate electronic balance, mercury thermometer (preferably 0.1 or 0.2 oC graduations) or electronic thermistor temperature probe, accurate electronic stop watch or clock.
Note on graphical analysis
To get the best value for the temperature change (ΔT) you should take multiple readings before and after mixing the reactants and then plotting a graph versus time.
Above are two graphs from simple calorimeter experiments (picture on right).
On the left are typical results from an exothermic reaction e.g. metal plus acid or metal plus metal salt displacement reaction.
On the right are typical results from an endothermic change e.g. when certain salts dissolve in water.
The initial readings give you a baseline, but the reaction may take a few seconds or a few minutes, and so you cannot get an immediate true ΔT. However by drawing a baseline for the initial temperature and extrapolating back to the start of the reaction (e.g. at 1.5 minutes) you can then estimate the real temperature change.
What happens is quite simple, but it leads to inaccuracy:
For exothermic reactions the system will continuously lose heat once the reaction has started, so the temperature starts to fall once the reaction is complete, so extrapolating back up gives the true temperature rise.
In this case ΔT (corrected) = 28.4 - 20.4 = 8.0oC
For endothermic reactions the system will continuously gain heat once the reaction has started, so the temperature starts to rise once the reaction is complete, so extrapolating back down gives the true temperature fall.
In this case ΔT (corrected) = 19.5 - 11.2 = 8.3oC
Without allowing for these unavoidable experimental circumstances, you will always measure too low a temperature change.


No comments:
Post a Comment